Abstract
The existence and use of Harappan linear units have remained a riddle. Harappan town planning, in particular, has not so far been known to have used precise units, although it displays elaborate geometry. This article proposes that the site of Dholavira, in the Rann of Kachchh, enables us to calculate a possible linear unit used to lay out the fortifications. This unit, which works out to 1.9 m, is then related to a proposed Harappan angula of 1.76 cm, with a factor of 108 between the two, as indicated in later classical literature. Besides other Harappan sites, independent research at early historical and historical sites and structures- e.g., Taxila, Shishupalgarh, Thimi and the Delhi Iron Pillar is quoted as confirmation of the proposed system – an important case of continuity between India’s two urbanizations.
Dholavira’s Plan and Proportions
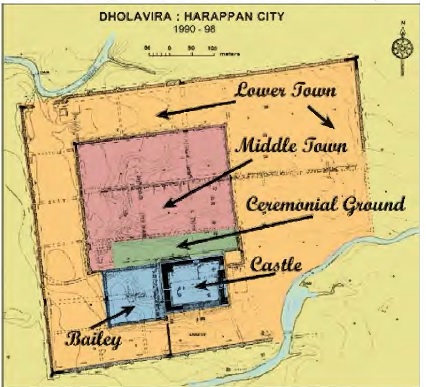
Dholavira (23°53’10″N, 70°13′ E) is probably the most spectacular Harappan site to be seen after Mohenjo-Daro, and, at 48 hectares, the second largest in India (after Rakhigarhi in Haryana). Discovered by the late Jagat Pati Joshi in the 1960s on the Khadir Island of the Rann of Kachchh, it was excavated in the 1990s under the direction of R.S. Bisht of the Archaeological Survey of lndia. The Harappans’ motivations in setting up this large city in such a harsh and forbidding environment must have been intimately related to access to raw materials, craft production and trade. There is evidence that the Rann of Kachchh was navigable in Harappan times, which would have given Dholavira access to the sea.[1] As a regional capital Dholavira must have exerted a measure of control over the hundreds of smaller Harappan sites dotting Kachchh, Saurashtra and mainland Gujarat. It flourished during the Mature Harappan phase, that is, between 2600 and 1900 BCE. Even if the climate might have been slightly more congenial than it is today, the establishment of such a city in this location is a feat of planning, engineering, labour control and execution, especially in the field of water harvesting and management: Dholavira’s colossal water structures, covering some 17 hectares and often interconnected through underground drains, were the sine qua non of the city’s survival through the year.
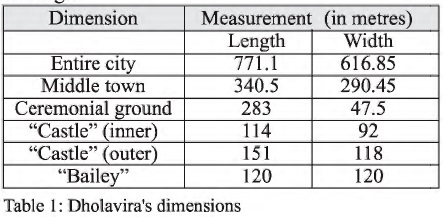
Like most Harappan sites, Dholavira followed a strict plan, but one of its kind with multiple enclosures. While Harappan town-planning is often based on an acropolis I lower town duality (as at Mohenjo-Daro and Kalibangan), Dholavira’s plan (Fig. 1) is triple: an acropolis or upper town consisting of a massive “castle” located on the city’s high point and an adjacent “bailey”; a middle town, separated from the acropolis by a huge ceremonial ground; and a lower town, part of which was occupied by a series of reservoirs. (Terms such as “castle”, “bailey”, etc., are those of the excavator.)
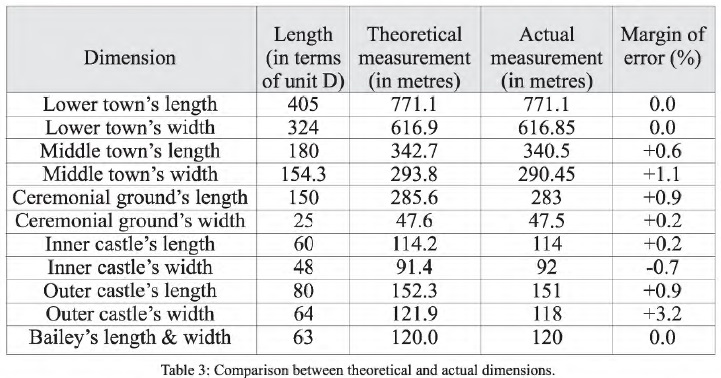
A mere look at the plan suggests a complex conceptual background. Can we make some sense of the concepts and rules Dholavira’s urban architects followed? To do so, we need to study the dimensions of the various fortifications, which were precisely measured by the ASI team. Table 1 summarizes them,[2] with a maximum margin of error of 0.5%.[3] Importantly, the three longest dimensions have since been confirmed by GPS readings.[4]
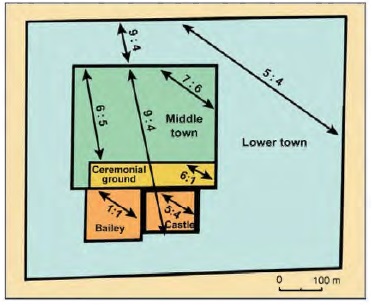
 It became immediately clear to the excavator that these dimensions obeyed precise ratios or proportions. Bisht highlighted some of them as follows (I have added in parentheses the margins of error calculated on the basis of Table 1 and rounded off to the first decimal):
It became immediately clear to the excavator that these dimensions obeyed precise ratios or proportions. Bisht highlighted some of them as follows (I have added in parentheses the margins of error calculated on the basis of Table 1 and rounded off to the first decimal):
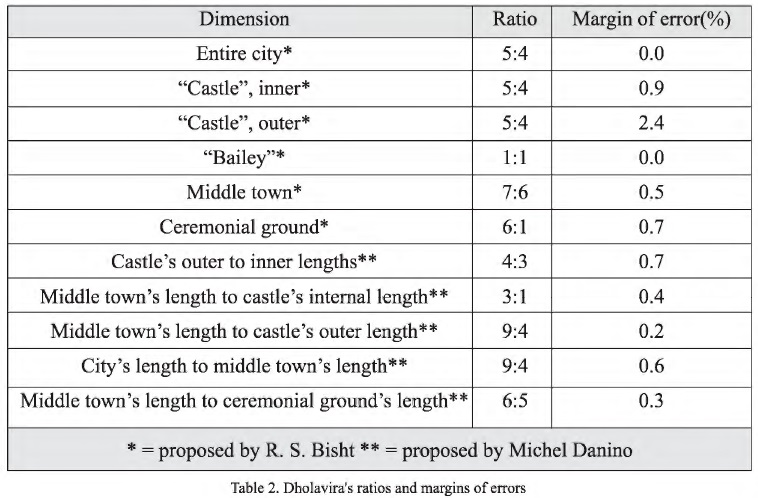
- The city’s length (east-west axis) and width (north south) are in a ratio of 5:4 or 1.25 (0.0%, a perfect match).
- The “castle” also reflects the city’s ratio of 5:4 (0.9% inner, 2.4% outer).
- The “bailey” is square (ratio 1:1).
- The middle town’s length and breadth are in a ratio of 7:6 (0.5%).
- The ceremonial ground’s proportions are 6:1 (0.7%).
All but one ratios are verified within 1%, an excellent agreement considering the irregularities of the terrain. In two papers,[5] I worked out a few other important ratios at work in Dholavira, some of which would have been chosen by the town-planners in order to define the whole city geometrically, others following as consequences of those initial choices. The principal ratios are summarized in Table 2 and Fig. 2. Not only are the margins of error very small, but the repetition of ratios 5:4 and 9:4 cannot be accidental.
Dholavira’s Master Unit of Length
How were Dholavira’s town planners able to impose such a set of precise ratios and dimensions on the ground? Two assumptions appear reasonable at this stage: (1) they must have used a standard of length; (2) they chose integral (or whole) multiples of this standard for as many of the main dimensions as possible. I propose that there is a simple way to calculate the main linear unit used at Dholavira.
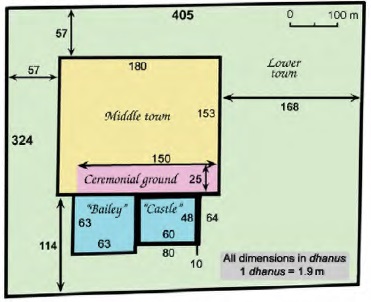
Let us call it “D” for Dholavira. Elsewhere,[6] I used a simple procedure to calculate the largest possible value of D that will result in most of the city’s dimensions being expressed as integral multiples of D. The procedure, briefly put, consists in algebraically expressing the smallest dimension in our scheme (i.e., the average width of the castle’s western and eastern fortifications) as a multiple of the unknown unit D ( or nD, n being an integer); then, using all available ratios, to express all larger dimensions in terms of nD. We find, of course, that a few dimensions are not integral but fractional expressions of nD. To make those fractions disappear, we choose “n” as the least common multiple of their denominators. It turns out that with n = 10, all fractional results disappear, except one. Going back to our initial formula, the width of the castle’s western and eastern fortifications, which we expressed as nD, is now 10 D. Bringing into play the proportions listed above, we can express all but one dimensions as multiples of D. Fig. 3 summarizes the findings.
We now only need to determine the value of D, which is simply derived from the city’s length: if771.1 m = 405 D, then D = 1.904 m or 190.4 cm, which we may round off to 1.9m.
Starting from this value and calculating the theoretical dimensions backward using Fig. 3, we can compare them with the actual dimensions. Table 3 lists the results, as well as the margins of error between theoretical and actual dimensions. The latter are remarkably modest, 0.6% on average (the highest being, again, in the outer dimensions of the “castle”). These almost perfect matches appear to rule out the play of chance.
Ratios in Harappan Settlements
For whatever reasons, Harappans clearly preferred certain fixed ratios to random proportions. This is visible not just at Dholavira but at other Mature Harappan sites, as the following selective list shows (in increasing order):
* Ratio 7:6, the ratio of Dholavira’s middle town, is found in the dimensions of the “assembly hall”, also called “pillared hall”, on the southern part of Mohenjo-Daro’s acropolis, which measures “approximately 23 by 27 metres.[7]
* Ratio 5:4, Dholavira’s prime ratio, is found elsewhere in Gujarat at Lothal, whose overall dimensions are 280 x 225 m,[8] and Juni Kuran Gust forty kilometres away from Dholavira in Kachchh), whose acropolis measures 92 x 72 m,[9] which approximates 5:4 by 2.2%. It is also reflected in Harappa’s “granary”[10] of 51:2 ~40.8 m (wit~ a precision of 0.3%) and in a major building of Mohenjo-Daro’s HR area[11] measuring 18.9 x 15.2 m (0.5%). Ratio 5:4 is repeated in other ways. At Dholavira, for instance, there are 5 salients on the northern side of the middle town’s fortification, against 4 on 1ts eastern and western sides (if we include the corner salients, their numbers grow to 7 and 6, which reflect the middle town’s ratio). Returning to Mohenjo-Daro’s “pillared hall”, it had four rows of five pillars each.[12] It is quite intriguing that this hall, in its dimensions (7:6) as well as rows of pillars (5:4), should reflect Dholavira’s two key ratios!
* Ratio 4:3 is visible in Mohenjo-Daro’s “granary” (also called “warehouse”): this structure is composed of 27 brick platforms (in 3 rows of 9); while all platforms are 4.5 m wide (in an east-west direction), their length (in a north-west direction) is 8 m for the first row, 4.5 m for the central row, and 6 m for the third row.[13] It is singular that both pairs (8, 6) and (6, 4.5) precisely reflect the ratio 4: 3.
* Ratio 3:2 is the overall ratio of Kalibangan’s lower town (approximate dimensions 360 x 240 m),[14] as well as of a sacrificial pit (1.50 x 1 m).[15] It is also the ratio of three reservoirs at Dholavira: one in the “castle” measuring 4.35 x 2.95 m,[16] and two larger ones to the south of the castle.[17] We find it again (within 1%) at Mohenjo-Daro in the overall platform of the “granary” which measures 50 x 33 m.[18]
* Ratio 2: 1 is that of Dholavira’s acropolis (“castle” and “bailey” together); it is also found at Mohenjo-Daro[19] (whose acropolis rests on a huge brick platform measuring 400 x 200m), Kalibangan[20] (acropolis of 120 x 240m) and Surkotada[21] (overall dimensions 130 x 65 m).
* Ratio 9:4, apart from its double presence at Dholavira is found at Mohenjo-Daro’s long building located just north of the Great Bath, called ‘”block 6″ and measuring approximately 56.4 x 25 m,[22] thus within 0.3%.
*Ratio 7:3 is found at Harappa’s mound AB in “14 symmetrically arranged small houses”,[23] each measuring 17.06 x 7.31 m (nil margin).
* Ratio 5:2 is that of Dholavira’s colossal eastern reservoir[24] (73 .5 x 29.3 m, thus with a margin of 0.3%), Fig. 4. It is also reflected, with the same high precision, in 12 rooms of Harappa’s “granary”, each measuring 15.2×6.1 m.[25]
* Ratio 11:4 is that of the secondary rock-cut reservoir “SR3”[26] found to the south of the Dholavira’s “castle”, 15.5 x 5.65 m, with a high degree of precision (0.2%), Fig. 5.
* Ratio 3:1 is found at Mohenjo-Daro’s “college” whose average dimensions are 70.3 x 23.9 m.[27]
* Ratio 7:2 is that of Dholavira’s primary rock-cut reservoir “SR3”[28] mentioned above (33.4 x 9.45 m, thus with a margin of 1%), Fig. 5.
* Ratio 6:1 is reflected not just in Dholavira’s ceremonial ground but in Lothal’s dockyard[29] (average dimensions 216.6 x 36.6 m).
The above few examples are summarized (with a few more) in Fig. 6. In probabilistic terms, while lower ratios (such as 7:6) could be rejected as a rough approximation of 1 and therefore of no particular significance, the higher we rise in the scale and the less tenable such an explanation will be: the intentional use of specific proportions is indisputable and has not attracted sufficient attention so far. Harappan architects and builders did not believe in haphazard constructions, but followed precise canons of aesthetics based on specific proportions.
We can also see that Dholavira’s ratios are not exclusive to this site but are part of a broader Harappan tradition of town planning and architecture, whose conceptual foundations remain poorly understood.

Fig. 6: A sampling of ratios found at a few Harappan sites (on a linear scale), generally with a high degree of
precision.
Notes
[1] Michel Danino, The Lost River: On the Trail of the Sarasvati, Penguin Books, New Delhi, 2010, p. 165 and references cited.
[2] R.S. Bisht, “Dholavira Excavations: 1990-94”, Facets of Indian Civilization: Essays in Honour of Prof B.B. Lal, ed. J.P. Joshi, Aryan Books International, New Delhi, 1997, val. I, pp.107-120; “Dholavira and Banawali: Two Different Paradigms of the Harappan Urbis Forma”, Puratattva 1999, 29: 14-37; “Urban Planning at Dholavira: a Harappan City”, in Ancient Cities, Sacred Skies: Cosmic Geometries and City Planning in Ancient India, eds. J. McKim Mal ville & Lalit M. Gujral, Indira Gandhi National Centre for the Arts & Aryan Books International, New Delhi, 2000, pp. 11-23.
[3] R.S. Bisht, “Urban Planning at Dholavira: a Harappan City”, op. cit.,p. 18.
[4] Michel Danino, “Further Research into Harappan Metrology at Dholavira”, Man and Environment, val. XXXV, no. 2, 2010 (in press).
[5] Michel Danino, “Dholavira’s Geometry: a Preliminary Study”, Puratattva 2005, 35: 76-84; “Unravelling Dholavira’s Geometry”, in Rama VTjayam: Recent Researches in Archaeology, History and Culture (Festschrift to Prof K. V. Raman), P. Chenna Reddy, ed., Agam Kala Prakashan, Delhi, 2010, pp. 179-193.
[6] Michel Danino, “Unravelling Dholavira’s Geometry”, op. cit.
[7] Gregory L. Possehl, The Indus Civilization: A Contemporary Perspective, AltaMira Press, Walnut Creek, 2002; reprint Vistaar Publications, New Delhi, 2003, p. 194.
[8] B.B. Lal, The Earliest Civilization of South Asia, New Delhi: Aryan Books International, 1997, p. 129.
[9] Dilip K. Chakrabarti, The Oxford Companion to Indian Archaeology: The Archaeological Foundations of Ancient India, Oxford University Press, New Delhi, 2006,p.166.
[10] Ernest Mackay, Early Indus Civilization: Ancient Cities of the Indus Plains, 2nd ed., 1948, repr. Eastern Book House, Patna, 1989,p.45.
[11] Madhukar K. Dhavalikar & Shubhangana Atre, “The Fire Cult and Virgin Sacrifice: Some Harappan Rituals” in Old Problems and New Perspectives in the Archaeology of South Asia, ed. Jonathan Mark Kenoyer, University of Wisconsin, Wisconsin, 1989,pp. 195-97.
[12] Michael Jansen, “Mohenjo-Daro: architecture et urbanisme”, Les cites oubliees de /’Indus: Archeologie du Pakistan, Jean-Francois Jarrige, ed., Association francaise d’action artistique & Musee national des Arts asiatiques Guimet, Paris, 1988,p. 137.
[13] Michael Jansen, “Architectural Problems of the Harappa Culture,” South Asian Archaeology 1977, ed. Maurizio Taddei (Naples: Istituto Universitario Orientale, Seminario di Studi Asiatici, 1979), vol. 1,p. 420.
[14] B.B. Lal, India 1947-1997: New Light on the Indus Civilization, Aryan Books International, NewDelhi, 1998, p.l19.
[15] Ibid.,p.96.
[16] Ibid.,p.43.
[17] Michel Danino, “Further Research into Harappan Metrology at Dholavira”, op. cit.
[18] Michael Jansen, “Architectural Problems of the Harappa Culture”,op. cit.,p. 420.
[19] Michael Jansen, “Mohenj o-daro: architecture eturbanisme”,op. cit. ,p.134.
[20] B.B. Lal, The Earliest Civilization of South Asia, op. cit., p. 122.
[21] Ibid.,p.135.
[22] E.J.H. Mackay, Further Excavations at Mohenjo-Daro, Delhi: Government of India, 1938; Republished New Delhi: Munshiram Manoharlal, 1998, vol.1,p.17.
[23] Dilip K. Chakrabarti, The Oxford Companion to Indian Archaeology, op. cit.,p.156.
[24] Michel Danino, “Further Research into Harappan Metrology at Dholavira”, op. cit.
[25] Jonathan Mark Kenoyer,Ancient Cities of the Indus Valley Civilization , Oxford University Press & American Institute of Pakistan Studies, Karachi & Islamabad, 1998, p. 64.
[26] Ibid.
[27] E.J.H. Mackay, Further Excavations at Mohenjo-Daro, op.cit.,p.10.
[28] Ibid.
[29] S.R.Rao, Lothal, a Harappan Port Town (1955-62), Archaeological Survey of India, New Delhi, 1979, vol. 1, p. 123.
To be continued …
This article was first published in Propagation: A Journal of Science Communication and has been republished with the permission of the author.
Disclaimer: The opinions expressed within this article are the personal opinions of the author. IndiaFacts does not assume any responsibility or liability for the accuracy, completeness, suitability, or validity of any information in this article.
Michel Danino is a French-born Indian scholar of ancient Indian civilization, history and culture. He authored The Lost River: On the Trail of the Sarasvati (Penguin Books, 2010) and Indian Culture and India’s Future (DK Printworld, 2011). He recently edited Sri Aurobindo and India’s Rebirth (Rupa, 2018). He has taught aspects of Indian civilization in several educational institutions; his lecture series at IIT Kanpur recorded over 200,000 views. Since 2011 he has been associated with IIT Gandhinagar, where he is visiting professor and coordinates the Archaeological Sciences Centre.