In the previous article we read about one of the great misconceptions in Indian astronomy, namely, the tilt or obliquity of the earth’s axis, and how the European colonial scholars of yesteryear managed to obfuscate the ancient Indian value as an imprecise 24°, when it was actually 23.975°.
In this article, we move on to the topic of Wonders in Indian astronomy.
There are actually dozens of items in Indian astronomy, big and small, that would easily qualify as a wonder. Of those many marvels, let us examine in this article a wonder, which, in my opinion, is perhaps the most astonishing of all.

Wonder # 1 – The Pulsating Indian Epicycle
Some Background
Today it is common knowledge that the Sun is the center of the solar system, and that the planets move around it in orbits of elliptical shape.
Ancient man, quite obviously, was unaware of these modern discoveries. When he looked up at the sky, he beheld a vast dome (an inverted bowl, in the words of Khayyam) on which were stuck a fascinating array of objects – the sun, the moon, the planets, myriads of stars, and the occasional comet or meteor whizzing by.
He noticed that every few hours the sky changed its position, and it occurred to him that this enormous dome was actually rotating in a circular fashion around his home (the earth) carrying with it the sun, the moon and the planets. Today, of course, we know that the apparent rotation of the sky is an illusion caused by the rotation of the earth on its axis.
Anyways, sometime later, when our ancient ancestor looked more carefully at the sky, and made some rudimentary measurements, he was puzzled by what he found.
While the stars appeared to have a perfectly uniform circular motion around the earth, other objects in the sky, like the sun, the moon and the planets, did not. These latter bodies seemed to have an independent and strange motion of their own.
At times these bodies appeared to be nearer (they looked a little larger), and at other times farther away (they looked smaller). Sometimes they were moving slowly, and at other times faster. And, most perplexing of all, at times some planets were seen to stop moving, and go in reverse (backwards)!
What could possibly be causing such an irregular motion of these bodies? Why were they not moving in nice, uniform, circular orbits like the stars? His curiosity, no doubt, impelled him to investigate and speculate on the reasons for this. But, for a long time, the problem was beyond his understanding.
Eventually though, when his mathematics and geometry had advanced sufficiently, he developed an ingenious geometric model, the so-called EPICYCLE-SYSTEM, which, believe it or not, very neatly explains all these variations in speed, proximity and direction of these heavenly bodies.
We will examine the epicycle-system shortly, but, before we step into that, it must be mentioned that the subject of epicycles is today a contentious area, with plenty of accusations and acrimony. European scholars have been claiming for the past 200 years that it was the Greeks who invented the epicycle-model, and that the Indians copied it from them. Indian scholars are now beginning to challenge that. Hopefully, by the end of this article, readers will have enough information to form a knowledgeable opinion of their own.
Before we take up epicycles, an understanding of the elliptical orbit is essential.
The Ellipse
The ellipse is a geometric figure that looks like a squished circle, which mathematicians find utterly fascinating.
Fig. 1A shows a circle and its center. Now imagine that you grabbed hold of that circle by its left and right sides, and pulled it apart a little. You would end up with something like Fig. 1B.
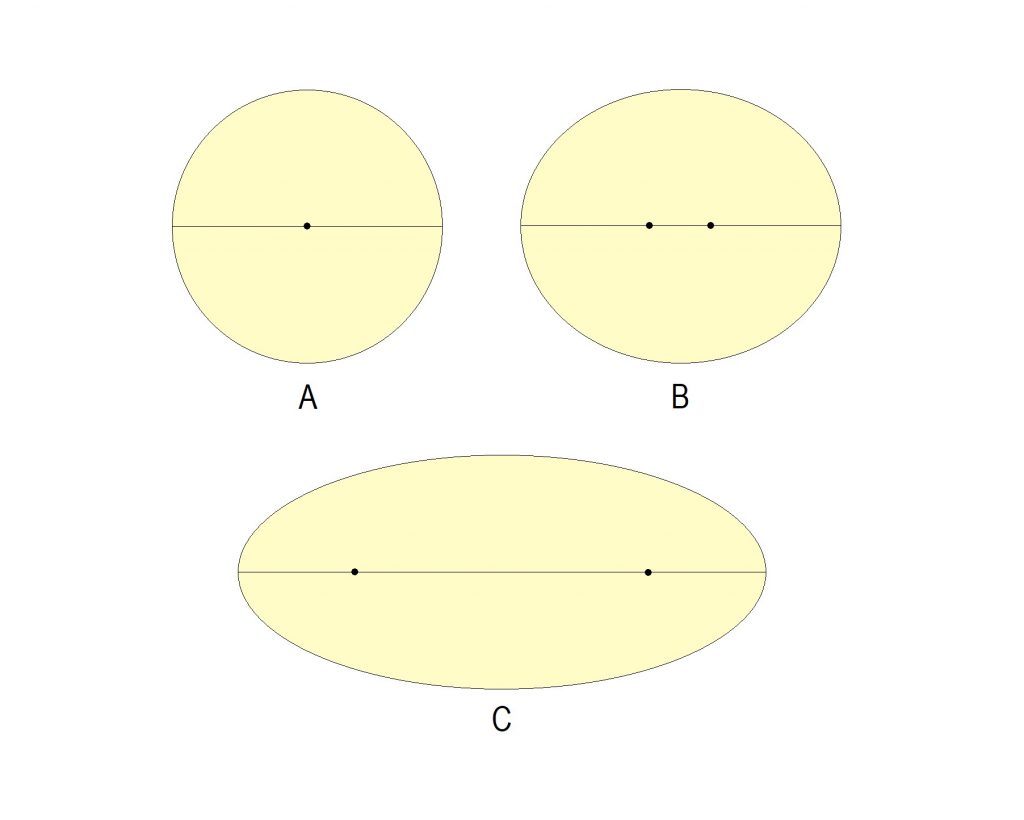
Notice that not only is the circle now an oval, but your pulling also split the center into two centers. An ellipse is an oval with two centers, also called two focuses, or foci (plural). If you kept pulling, the ellipse would become more eccentric, and the foci more apart, as seen in Fig. 1C.
As an aside, note that the ellipse holds a special pride of place for India. Great mathematicians of the past, including the likes of Kepler and Euler, have struggled to find a formula that would give the exact boundary length (perimeter) of the ellipse. Ramanujan in 1914 provided the most accurate approximation till date, and shortly thereafter improved it further with a second approximation. Today, there are exact formulas to calculate the perimeter, but these are all based on infinite series, which are computationally cumbersome, and end up being approximate anyway, because it is practically impossible to compute an infinite number of terms. Ramanujan’s two formulas are elegant, concise, and used ubiquitously in most modern computations of the ellipse.
To give you an idea of the accuracy of these formulas, consider this. If Pluto’s orbit was exactly elliptical, you could use Ramanujan’s second formula to find the perimeter of its orbit (of billions of kilometers) with an error of less than one-thousandth of a millimeter1. Incredible!
The Elliptical Orbit
In the field of astronomy too the ellipse holds a special place of honor. Any object gravitationally bound to another (i.e. in orbit around it) will always move in an elliptical orbit.
The earth, the moon, the planets, the binary-stars, and even the satellite which an ISRO rocket hurls into space, all move in elliptical orbits.
Let us briefly examine the elliptical orbit, taking the Moon as an example.
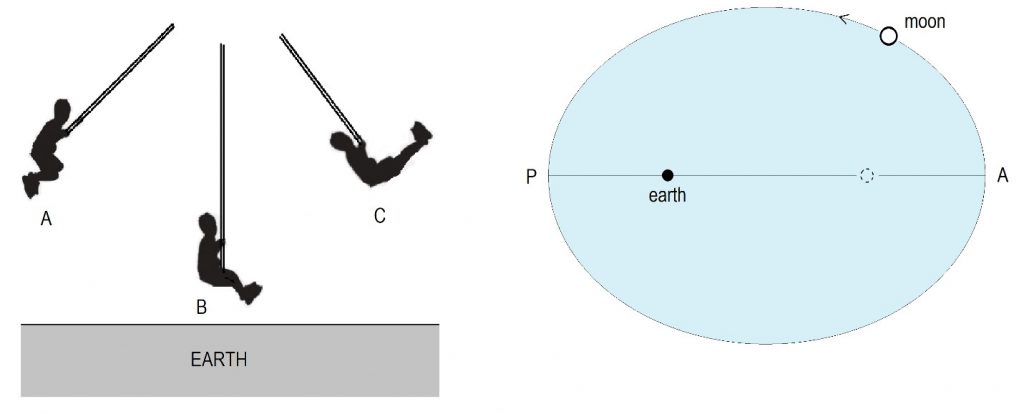
The left side of Fig. 2 shows a child on a swing. There is an interesting energy transformation taking place here. At points A and C, the swing is at its highest, or farthest, from the earth. At these points its kinetic energy (speed) is the lowest, while its gravitational potential energy (height) is maximum. At point B, the reverse is true; there the swing is moving at its maximum speed (highest kinetic energy) while its gravitational potential energy (height) is the lowest. As the swing moves to and from, there is a constant energy transformation taking place, from kinetic to potential (speed to height), and vice-versa.
A very similar thing occurs in an elliptical orbit, as shown on the right side of the figure. Observe that the earth is at one focus of the Moon’s elliptic orbit, while the other focus is empty. The Moon comes closest to the earth at the Perigee (P), and is farthest at the Apogee (A). At P, its distance from the earth (or height) is minimum and its speed is maximum. At A, the opposite is true; it has a maximum height and a minimum speed. Like the swing, the Moon’s kinetic and potential energy (speed and height) are constantly being transformed from one to the other as it moves around its elliptical orbit.
As an aside, note that the eccentricity of the Moon’s orbit has been exaggerated in Fig. 2 for instructional purposes. In reality, the Moon’s orbit is quite close to a circle, with only a small eccentricity.
Anyhow, now that we have examined the elliptical orbit, let us return back to our ancient ancestor, who was puzzled by the movement of the Moon.
Obviously (he reasoned), the Moon was not moving in a uniform circular orbit, because it was clearly closer at times, and farther away at other times. Also, when it was closer its speed was higher, and when it was farther away its speed was slower.
Now, what kind of a geometric model could possibly account for these variations?
After a long struggle, he hit upon a brilliant solution!
The Epicycle
What exactly is an epicycle? In simple terms, an epicycle is a circle moving on another circle.
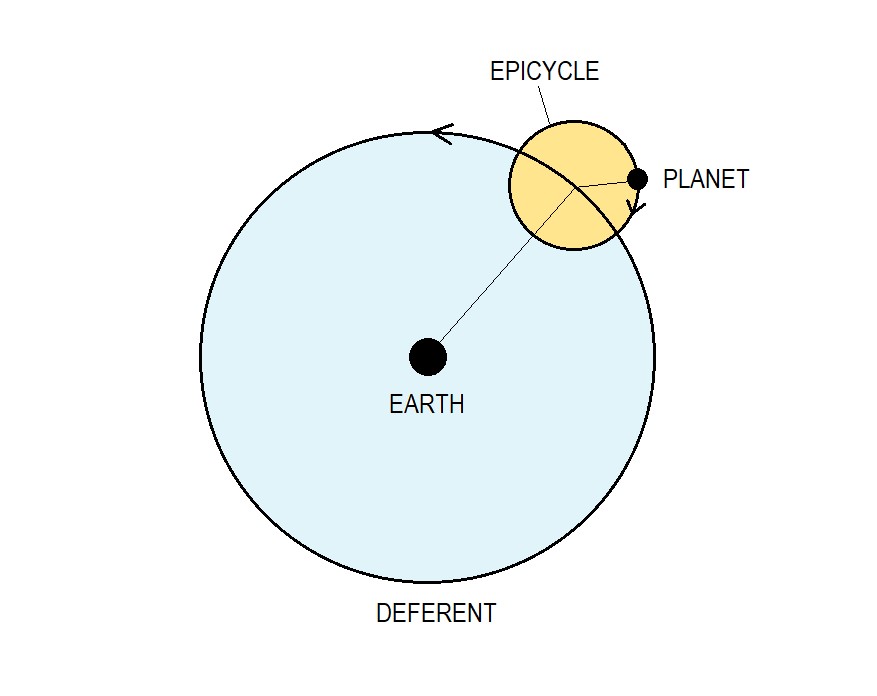
As shown in Fig. 3, the bigger (blue) circle, with the earth at its center, is called the Deferent. The smaller (orange) circle is the Epicycle. The planet moves around the epicycle, while the epicycle itself travels around the deferent.
Now, at first sight, you might not be too impressed by this; but wait till you see it in action!
Try it yourself
To give you an idea of the power of the epicycle, I created a couple of interactable movies using Adobe Flash.
To try the epicycle yourself, please go to this link and download two movies: Epicycle.swf and Pulsation.swf. Clicking on the files will take you to a download page. Click the download button and the file will be downloaded to your computer.
These movies need Adobe Flash Player to run. There are two ways to handle this. The easiest way is to use your browser. Open your browser and drag-and-drop the .SWF movie into it. You may be asked if you wish to activate Flash Player, or download an extension. Say yes. In my experience Firefox handles this better than Google Chrome.
The other (harder) way is to install the free Adobe Flash Player on your computer. You can get it here. Remember to uncheck any ‘special offers’ from Abobe before downloading and installing.
When you are finally able to run the Epicycle.swf movie, you should see the below:
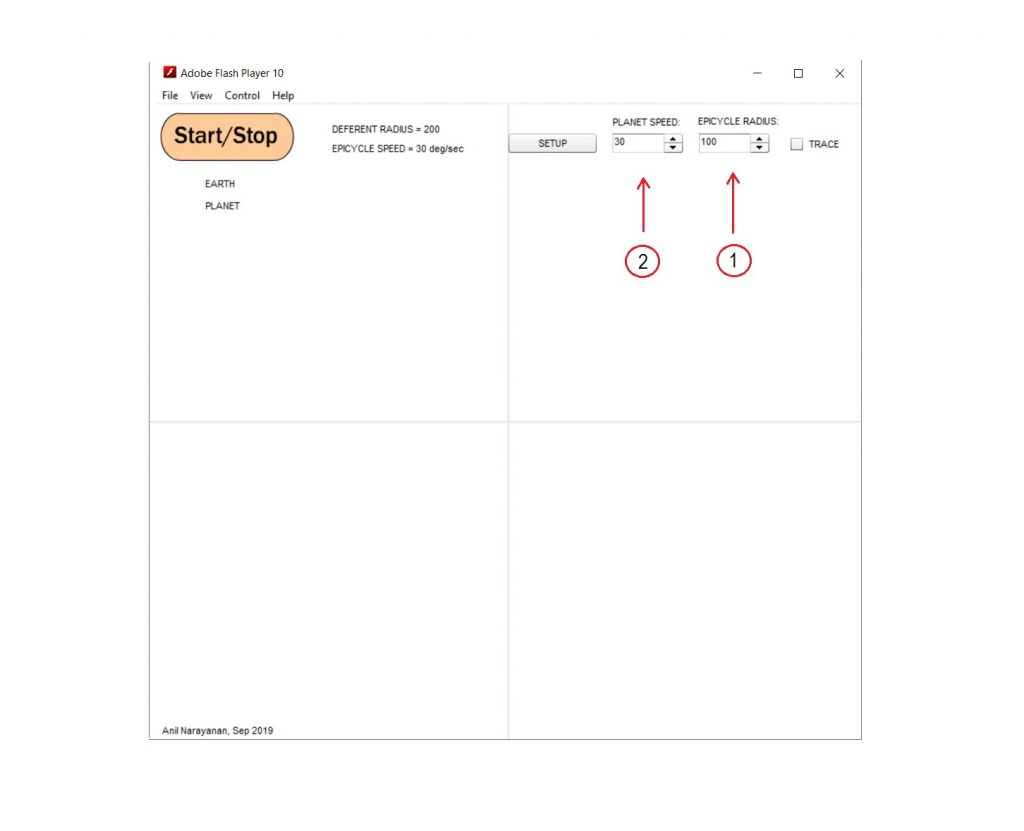
There are 4 parameters in the epicycle-model: 1) Deferent radius, 2) Epicycle radius, 3) Epicycle speed, 4) Planet speed.
Of these four, we will keep two fixed (Deferent radius=200 and Epicycle speed=30 deg/second), and play with the other two (Planet Speed and Epicycle radius).
Click the ‘SETUP’ button, and you should see the model show up, ready to run, as below:
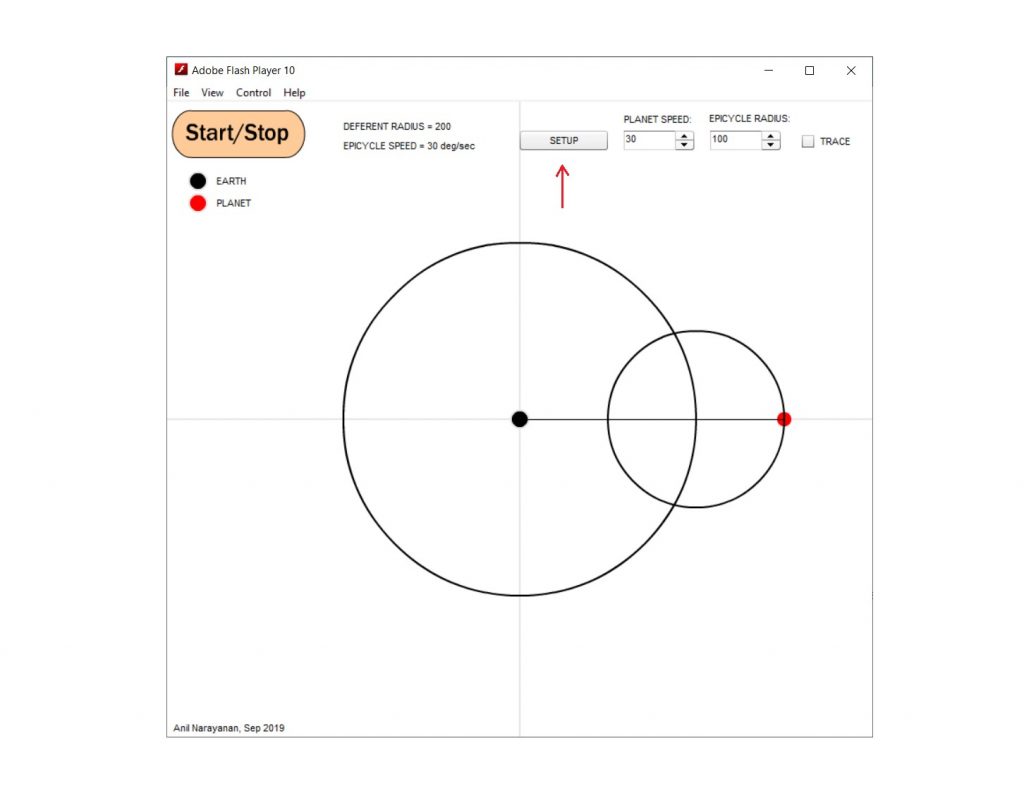
Click the ‘TRACE’ checkbox on the right, to have the planet leave a green trail as it moves, so you can see the orbit shape.
Now click the ‘Start/Stop’ button. You should see the epicycle in action, as below:
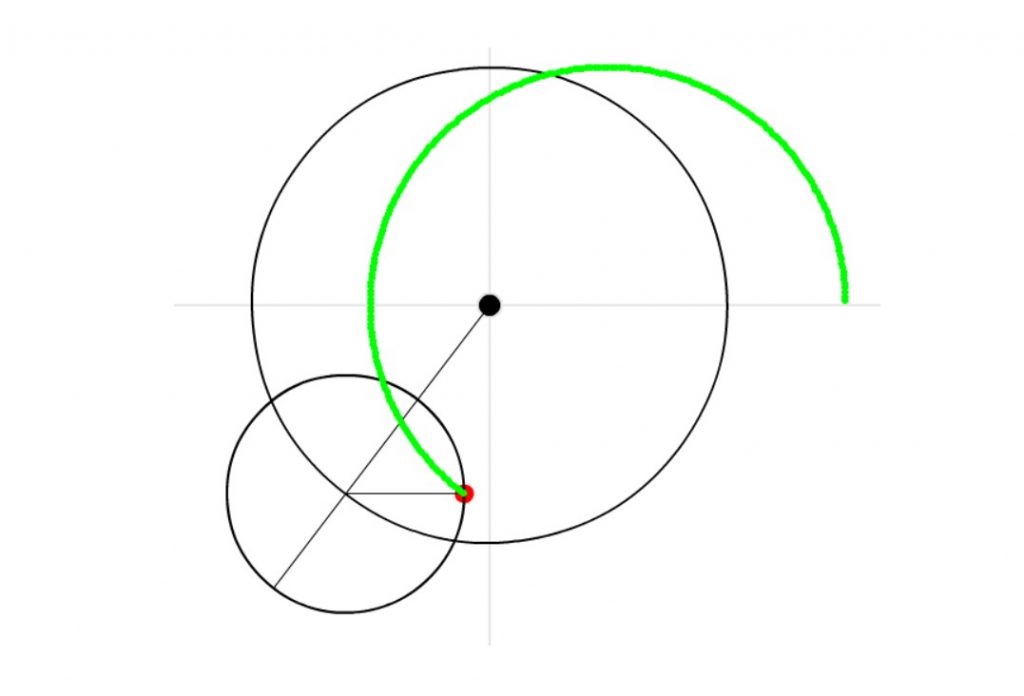
To try out various combinations, follow these steps:
- Open (double-click) Epicycle.swf
- Set the Epicycle Radius and Planet Speed to some values, as you like (note that Planet Speed can be negative as well, going counter-clockwise).
- Click the ‘TRACE’ checkbox
- Click ‘SETUP’ to create the Model
- Click the Start/Stop button to start the epicycle and see the planetary orbit you created with your setting.
You can click the Start/Stop button anytime to pause/resume the action.
Unfortunately, there is no easy way to restart the movie in Flash with a different setting. So, for each setting that you want to try, you have to close the file, and reopen it.
I was able to obtain some interesting orbits, as shown below. The settings are embedded in each figure (PS=Planet Speed, ER=Epicycle Radius).
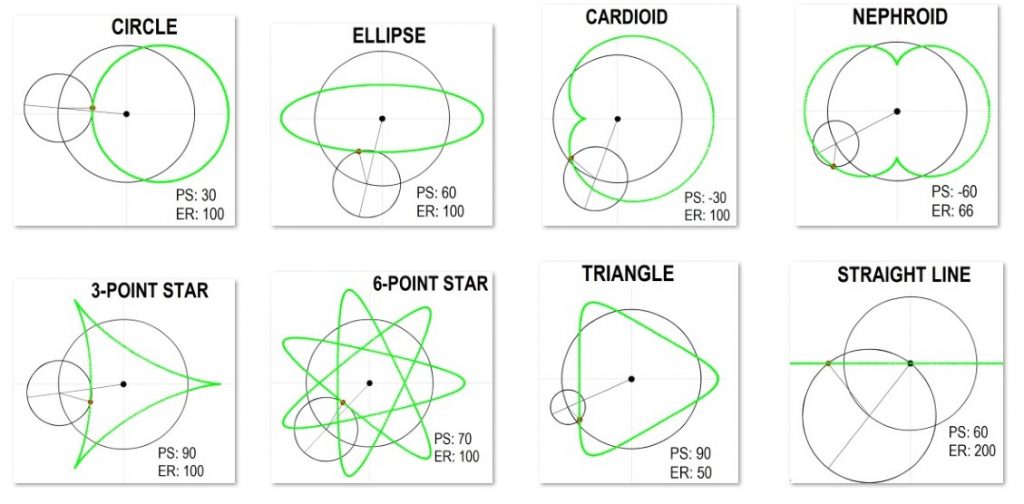
Surprisingly, it is even possible to obtain an orbit that is a perfect straight line!
Try out some settings of your own, and let us know if you created any interesting orbits, and what settings you used!
Hopefully, the reader is now sufficiently impressed by the power of the epicycle, and by the ingenuity of our ancient ancestors who created it (remember, they had no Adobe Flash!). Also note the fact that we have employed only a single epicycle so far, which is merely scratching the surface of this technique. Using multiple epicycles, almost any conceivable shape can be traced. Check out this link to explore deeper.
Moving on, let us see how the power of the epicycle was applied to astronomy, starting with the Greeks.
The Greek Epicycle
The Greek epicycle is very simple.
The two speeds, namely, that of the epicycle on the deferent, and of the planet on the epicycle, are set equal (but in opposite directions, one clockwise, the other counter-clockwise).
As seen in the first item in Fig. 7 above, such a setting results in a circular orbit. This circular orbit is shifted rightward of the deferent, so that the earth is not its center. Such a shifted circle is also called an ‘eccentric’ (an off-center circle), as shown in Fig. 8.
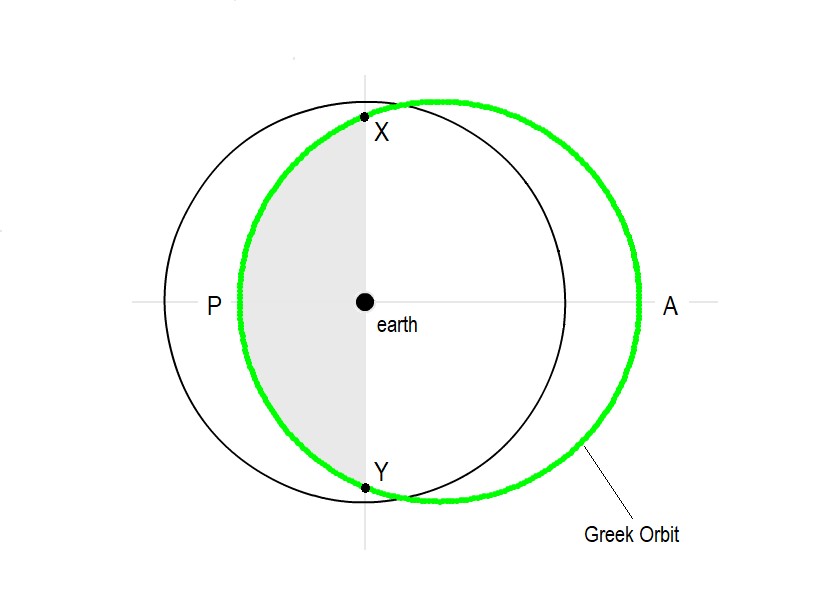
Does this eccentric orbit exhibit the same features as the elliptical orbit? Let us see.
At point P, we note that the eccentric orbit is closest to the earth, and at point A it is farthest. Well, that at least explains the variation in proximity (planet is sometimes near and sometimes far).
Further, we observe that the orbital fragment XPY is clearly smaller than the fragment XAY. But note that both these arcs are equal to 180 degrees (half the sky) as seen from the earth. That is, the planet takes lesser time to cover arc XPY, of 180 degrees, and more time to cover arc XAY, also of 180 degrees. In other words, as seen from the earth, the planet appears to move faster near the Perigee P, and slower at the Apogee A, which is exactly how an elliptical orbit behaves.
In summary, the Greek epicycle produces only a shifted (eccentric) circle, and not an ellipse or other complex shapes. While this is not great, it is not bad either, as the eccentric does simulate the main features of the elliptical orbit, namely, the proximity and speed variations.
The Indian Epicycle
The Indian epicycle shares the basic feature of the Greek epicycle, namely, the speed of the epicycle on the deferent is equal to the speed of the planet on the epicycle.
The similarities, however, end there. The Indian epicycle adds three levels of complexity on top of this, which puts it on a different plane altogether. Let us examine these added complexities.
Firstly, the epicycle radius is not a constant. So, the epicycle enlarges and shrinks (pulsates) as it moves on the deferent. Check out the Pulsation.swf movie to see the pulsating epicycle in action.
Secondly, the details of pulsation are surprisingly complex. All said and done, the epicycle is an ancient technique, created by ancient people. How intricate could such an ancient technique be? A linear variation of radius with angle would have been complex enough for this ancient technology, and yet, the actual variation of pulsation is far more complex – it is sinusoidal! Though we know the ancient Indians were advanced in mathematics and geometry, still, this extra bit of complexity comes as a surprise.
Thirdly, the direction of pulsation is not the same for all planets. This is an intricacy that is not easily explained in a non-technical forum, so I will not attempt it.
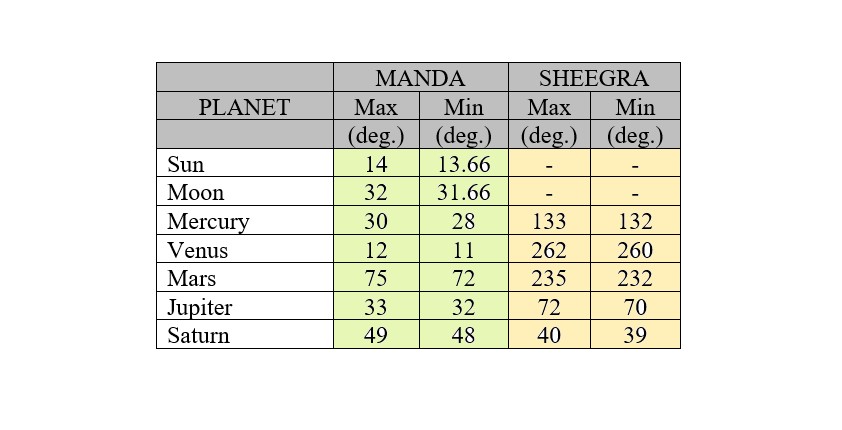
Apart from these complexities, another striking fact of the Indian epicycle system is the fine-ness of pulsation. Fig. 9 shows a Table of the maximum and minimum circumferences of the epicycle for each planet during pulsation. Manda and Sheegra are two kinds of Indian epicycles, which we won’t go into here.
From the Table we note that all of these pulsations are exceedingly fine – the epicycle size changes only a little, making minor adjustments to the final orbit. We are filled with wonder for whoever crafted such fine control of the planetary orbits!
To summarize, the pulsating Indian epicycle is laden with technical complexities that are far beyond the simple Greek epicycle. While the Greek epicycle creates only an eccentric circle, the Indian epicycle produces a very complex orbit that defies simple description. For small pulsations, the Indian orbit is close to an ellipse.
The Sun’s Orbit – Comparing Greek and Indian Epicycles
The proof of the pudding, it is said, is in the eating. To round out this discussion, let us compare Indian and Greek epicycle techniques by applying them to the simplest possible orbit (that of the Sun) and examine how well they predict its orbit.
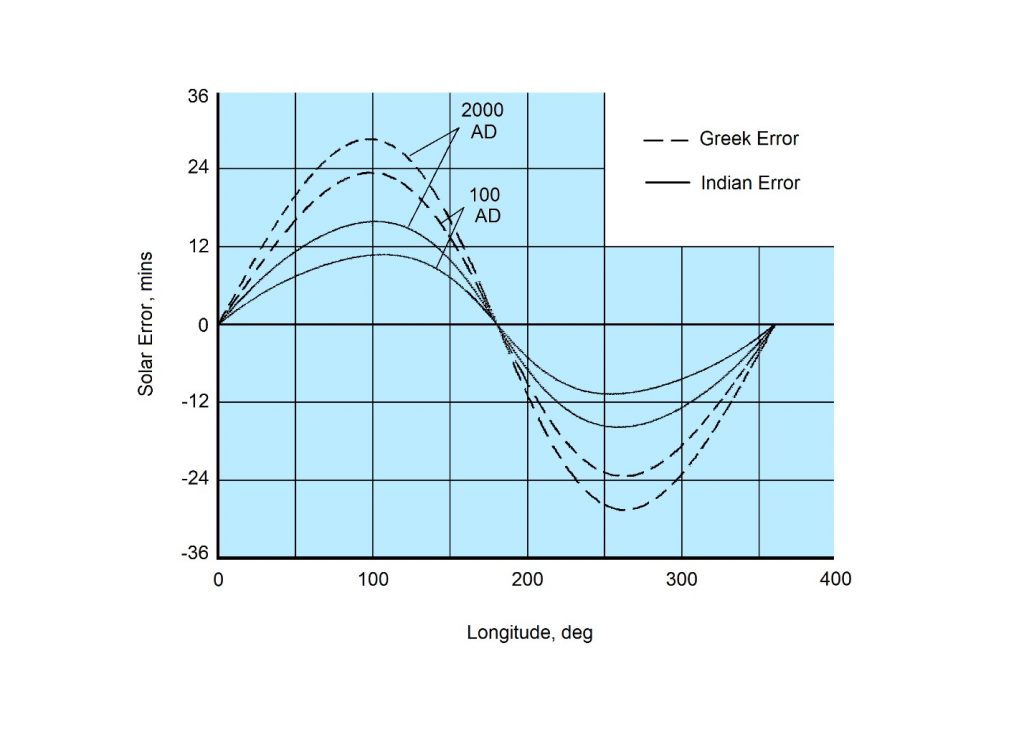
Fig. 10 shows the error in arc-minutes of Indian and Greek epicycles for the Sun, for the years 2000 AD and 100 AD2. It is seen that the Indian error for both dates is half that of the Greek. In other words, the Indian epicycle of the Sun is twice as accurate as the Greek.
Fig. 10 also shows another interesting fact. The Indian Epicycle of the Sun was more accurate 2000 years ago than it is today! This naturally raises the question – what if we go back further in time?
The results are shown in Fig. 11.
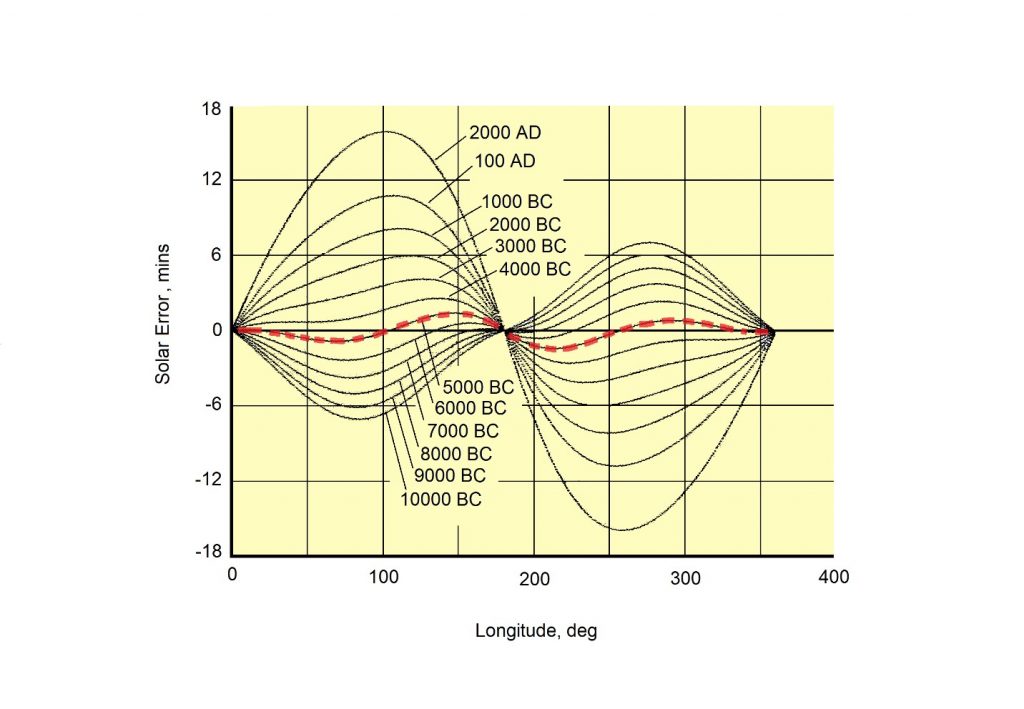
This figure highlights the interesting fact that the pulsating Indian epicycle of the Sun grows progressively more accurate (has less error) as we go back in time, reaching peak accuracy (minimum error) at about 5000 BC (red dashed line). Very curious!
Does that mean the Indian epicycle of the Sun was created in that timeframe (5000 BC)? Dare we make that conclusion? Is Indian astronomy that old?
Well, looking at the intricate design of the pulsating Epicycle, we can say for certain that the ancient Indian astronomer spent a lot of time tinkering and fiddling with his model. Why would anyone do that? Unless it was to make his model as close to reality as possible. If that line of reasoning is any good, then, applying a cushion on observational accuracy of say 5 minutes of arc, we can state that the pulsating Indian Epicycle of the Sun was developed somewhere in the period (8000 BC – 3000 BC).
Colonial attempts to downplay the Pulsating Indian Epicycle
As can be expected, the British colonial rulers and their evangelical brethren were anxious to keep a lid on this astounding feature of Indian astronomy.
The western translators of the Surya-Siddhanta quickly glossed over the matter like this …
A remarkable peculiarity of the Hindu system is that the epicycles are supposed to contract their dimensions as they leave the apsis or the conjunction, becoming smallest at the quadrature, then again expanding till the lower apsis, or opposition is reached.
Move along folks, nothing much here. Only a little Hindu peculiarity, that’s all.
And a few pages later, they would be writing paragraphs upon paragraphs proving that the Indians borrowed their epicycle from the Greeks!
The Situation Today
The situation today is little better than what it was 150 years ago, thanks to the complete hijacking of Indian astronomy by western historians during the 19th and 20th centuries. Here, for example, is what wiki (Elliptic Orbit) says on the Sun’s orbit …
The Babylonians (3000 BC) were the first to realize that the Sun’s motion along the ecliptic was not uniform…
The Babylonians never used any epicycles, much less a complex one like the pulsating Indian epicycle.
It would be nice if Indian astronomy got at least an ‘honorable mention’ in regards to the Sun’s orbit.
Wonder Summary
The Pulsating Indian Epicycle is one of the great wonders of ancient science. The very fine pulsations that are set into the Indian models for each planet indicate that the Indian epicycle system is the result of a long and sustained tinkering over time. It also implies that the Indian astronomer had access to a vast collection of very accurate data.
We salute the ingenuity of the ancient Indian astronomer, not only in observational technique, but also in devising the elegantly conceived pulsating epicycle.
Closure
Before we close, we must briefly discuss the thought unsaid, the elephant in the room. Was there any borrowing between the Indians and the Greeks?
After all, the epicycle is an idea, and two people, far away from each other, can have the same idea.
I will leave you with some points to consider:
- To develop a technique like the epicycle, with a complex twist to it like pulsation, needs a goodly amount of very accurate data, to verify the model at every step. Now, the Greeks had no data at all. I mean zero, zilch, nada. It is well accepted, even in the west, that the base Greek astronomy data was borrowed from Babylon, all of it.
- The current western spin is that the Indians borrowed the simple Greek epicycle, and then greatly improved it, with pulsation and other complexities. Now, that would imply the Indians had very accurate data, which is a contradiction of a pet western theory, that the Indians were poor observers, astronomically speaking.
- Alexander’s invasion of India occurred in 326 BC. Very shortly afterwards, I mean 5-10 years later, the Greeks had suddenly acquired a ton of mathematics (the 13 books of Euclid), apparently out of thin air.
- A few decades later, they also acquired the epicycle technique, which is credited to a gentleman named Apollonius of Perga, a mathematician at Alexandria in Egypt.
- A couple hundred years later, the great Greek astronomer Ptolemy wrote a book on geography that contains an astonishing amount of detail about the coast of South India, particularly Kerala.
References
- https://www.johndcook.com/blog/2013/05/05/ramanujan-circumference-ellipse/
- Narayanan, A., ‘The Pulsating Indian Epicycle of the Sun’, IJHS, 46.3 (2011).
Featured Image: Extreme Tech
Disclaimer: The opinions expressed within this article are the personal opinions of the author. IndiaFacts does not assume any responsibility or liability for the accuracy, completeness, suitability, or validity of any information in this article.
Anil Narayanan is former scientist at ISRO, now working as a consultant in Washington DC. His hobby is ancient astronomy to which he devotes most of his spare time. He is the author of the book ‘History of Indian Astronomy: The Siamese Manuscript’.

