Introduction
In the Indian tradition the seven notes of the saptaka are taken to be further subdivided into 22 srutis. The problem as to why this subdivision has 22 elements has concerned musicologists for a long time.[1] It is also not clear why the srutis are divided non-uniformly into groups of four, three, and two into musical notes in Bharata’s Natya Sastra (NS).
The saptaka, the “series of seven” is the same as the octave or the “series of eight” of Western music, spans a doubling of frequency. The seven notes of the saptaka are named sa (for sadja), ri (rsabha), ga (gandhara), ma (madhyama), pa (pancama), dha (dhaivata), and ni (nisada).
It must be said that we are speaking of a very old tradition. Manomohan Ghosh, who prepared the critical edition of NS and translated it, assigns it to about 5th century BC. He based his estimate on a variety of considerations.[2] These include linguistic usage, and the fact that Bharata speaks of an Arthasastra of Brhaspati and not of Kautilya, making him prior to the Mauryas.
Panini in his Astadhyayi (4.3.110-1) (c. 450 BC) speaks about Silalin and Krsasva as the authors of the Nata-sutras, which appears to have preceded the Natya Sastra. It seems that Bharata’s text was in the same tradition as Silalin’s, and the evidence indicating that Bharata preceded the Mauryas makes him a near contemporary of Panini. Their two works have similarity in that they analyze language – speech in the case of Panini and gesture, dance, and music in the case of Bharata – in terms of their primitives. One can see that these works could have appeared in the same intellectual atmosphere.
The Indian texts speak of three registers across three octaves. Within each register, there are three scales (grama): the sadjagrama, the madhya-magrama, and the gandharagrama. The third of these, the gandharagrama, is rarely referred to by Bharata suggesting that it had long ago gone out of use and that it represents an early scale used deities of the three gramas are Brahma, Visnu and respectively.
The notes are termed consonant (samvadin), assonant (anuvadin) and dissonant (vivadin), depending on the distance in srutis with respect to the sonant (vadin). According to NatS 28.22-23:
Notes that are at distance of 9 or 13 srutis from each other are mutually samvadin. Examples are sa and ma, sa and pa, ri and dha, and ga and ni in the sadjagrama. Similar is the case in the madhyamagrama, except that sa and pa are not consonant while pa and ri are.
The notes that are at the distance of two or twenty srutis are vivadin, for example ri and ga, dha and ni.
The vadin, samvadin and vivadin notes having been determined, the remaining notes are to be called anuvadin.
The mention of the distance between the samvadin and vivadin notes is helpful in the understanding of the measure of sruti, and we will return to this later. Another definition is provided in NatS 22.24 where it is said that in the madhyamagrama pancama should be made deficient in one sruti, and this is the standard in sruti.
Sarngadeva (century) his Sangita-Ratnakara (SR 1.3.10-22) tells us of how the seven notes can be produced on two twenty-two stringed vinas. One of the vinas is kept invariable and the other one is used in a variable mode. He shows how the notes one sruti apart merge. By this he establishes that there is a natural division into 22 audible pitch differences. But his method works because the number of stings in the vinas is 22, and it does not answer the more basic question of the number of microtones in a saptaka. One theory is that the division of the sruti provides a convenient division in terms of simple ratios. A combination of the cycle of fourths and fifths is invoked to generate 23 values from the twelve notes and the extra value of the fifth is dropped, leaving us with 22 values.
Considering the cycle of fifths, and ignoring the varying number of srutis amongst the notes, ri is fifth from pa (in the next octave). Since pa is midway through the octave (pa is 3/2), ri should be: 1/2×3/2×3/2=9/8. This, in turn, implies that ma should be 3/2× 8/9=4/3. The fourth from ma is ni, so it becomes 4/3 ×4/3 = 16/9. The fifth from ri is dha, so its value should be 9/8×3/2 = 27/16. Now ga can be calculated either as the fifth from dha or the fourth from ni and this gives us the values of 81/64 or 32/27.
This gives us the ratios upto the sa of the next octave:
(1,9/8,81/64,4/3,3/2,27/16,16/9,2) or
(1,9/8,32/27,4/3,3/2,27/16,16/9,2)
But there is no certainty that this reasoning was followed by the ancient musicologists. These ratios do not contain the small proportions 5/3 and 5/4, which are pleasing to the ear. It is plausible that ga was pegged at 5/4 and dha was fixed at 5/3. If that was the case then the difference in the ratios for dha would be 27/16× 3/5 = 81/80. We get the same difference at ga for one of the two values. This ratio is the comma.
Using the modified ratios for ga and dha we can generate new modified values for the other notes, and it has been argued that this leads to a total of 22 notes. But it is not clear what ratios of the seven notes were used in the ancient period, especially because a shift in the ratios appears to have occurred as the arched harp type of vina was replaced by the stickzither vina. But it is clear that the srutis did not represent a uniform division of the saptaka into 22 parts.
In the different reconstruction in various books and articles,[3] we have the ratios of:
(1,9/8,32/27,4/3,3/2,5/3,16/9,2)
(1,9/8,5/4,4/3,3/2,5/3,15/8,2)
(1,9/8,6/5,4/3,3/2,5/3,9/5,2)
(1,16/15,9/8,4/3,3/2,8/5,5/3,2)
(1,9/8,5/4,11/8,3/2,27/16,31/16,2)
(1,11/10,7/6,4/3,3/2,33/20,7/4,2)
Clearly, other choices can be made, especially since the sruti interval between the notes in not the same.
It has been suggested that the 22 srutis may be connected to the 7 notes via the value of π in a diameter to circle mapping. But no plausible theory for such a connection has been sketched. In particular, we cannot justify the specific non-uniform assignment of the sruti to the different notes in a diameter to circle mapping.
Another theory is that the number 22 is rather connected to the number of Rudras (11), where a multiplier of 2 is used to include the corresponding sakti. The plausibility of this theory becomes stronger when it is noted that the expanded list of srutis[4] totals 66, which will then equal twice the number of devatas mentioned in the Vedas. It is noteworthy that according to whe NS 29.23-74 there are 33 alankaras (ornamentations) in instrumental music.
The number associated with the earth and also with the sun in the Vedic literature is 21. The number 22 then represents a point that goes beyond the earth or the sun.
Still another possibility may be the connection with the number of ragas in each scale, which is 484 = 22^ 2 Might this knowledge have prompted the theorists to pick 22 as the number of subdivisions based on some numerical considerations? One or more than one of these reasons may have been behind the choice of the number 22.
In this note we investigate connections between Vedic chanting and the saptaka in the early texts prior to the Natya Sastra of Bharata Muni. In particular, we examine evidence from the Siksa texts and the Chandogya Upanisad, and we examine if the antecedents of the number 22 go before the time of Bharata.
More on the saptaka
The seven notes commencing with sadja are said to be produced respectively by the peacock, ox or cataka, goat, crane, blackbird, frog, and the elephant (SR 1.3.46). Each note can be low (mandra), medium (madhya), or high (tara).
Sarngadeva (SR 1.4.5) describes the rare use of the gandharagrama by saying that it is used in the heaven, and not in this world. There is no unanimity regarding the assignment of the srutis in the gandharagrama.
From each grama are derived a number of secondary scales (murchana). The names of the sadjagrama murchanas are: uttaramandra, rajan, uttarayata, suddhasdja, matsar krta, asvakranta, abhirudgata (SR 1.4.10-11). The first is the original scale, the remaining are the permutations. Thus rajani is ni sa ri ga ma pa dha.
The names of the madhyamagrama murchanas are: sauviri, harinasva, kalopanata, suddhamadhya, marg, paurav, hrsyaka. The gandharagrama murchanas are: nand, alapa, sukha, citravat, citra, sumukh, visala (SR 1.4.22-26).
Each grama is the foundation for pentatonic and hexatonic series of notes (tana), melodic line (varna), guration and ornamentation (alankara) and mode (jati).
Each note (like sa, ri,..) not only represents that particular frequency but also the interval from the preceding note upto that note. Thus sa represents the entire interval from ni to saThe notes that form the basic scale are called suddha ,notes lowered a sruti are called cyuta or komala (soft), and those raised by a sruti or two are called tivra (sharp), sadharana or kaisika (for one sruti) or antara or kakal(for two srutis). The altered notes are called vikrta SR 1.3.39-45 gives the following 19 notes that consist of 7 suddha and 12 vikrta notes[5]:
sadharana sa (1), cyuta ri (2), suddha ri (3), suddha ga (5), sadharana ga (6), antara ga (7), cyuta ma (8), suddha ma (9), sadharana ma (10), trisruti pa (12), suddha pa (13), kaisika pa (14), suddha dha (16), kaisika dha (17), suddha ni (18), kaisika ni (19), kakalni (20), cyuta sa (21) suddha sa (22).
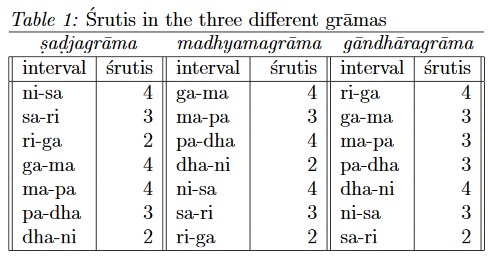
With this as the background, here is the traditional division of the srutis in the three different gramas, where the distribution for the gandharagrama is one reconstruction[6]:
It is noteworthy that in the sadjagrama the distribution of the srutis displays a symmetry about ma :4 ; 3 ; 2 = 4 = 4 ; 3 ; 2. This indicates that pa must have been at the precise ratio of 3 = 2 with respect to sa. This also means that the notes could not have been powers of a simple ratio and that vikrta notes must have been a part of the entire set from early on.
Sarngadeva says only the sadja- and the madhyamagramas are used in the world (dvau dharatale, SR 1.4.1). The gandharagrama must have fallen into disuse very early on. The names of the srutis given by Sarngadeva are as follows:
The srutis are divided into five classes:
1. dipta (dazzling): tivra, raudr, vajrika, and ugra
2. ayata (vast, extended): kumudvat, krodha, prasarin, sand pan, rohin
3. karuna (compassion): dayavat, alapin, madant
4. mrdu (tender): manda, raktika, priti, ksiti
5. madhya (moderate): chandovat, ranjan, marjan, raktik, ramya, ksobhin
The Vedic tradition
There is mention at several places in the Rgveda of singing.[7] The rcas were chanted in three notes: anudatta, svarita, and udatta, or “grave”, “medium”, and “acute”. Furthermore, there were the five saman notes prathama, dvitiya, trtiya, caturtha, and mandra. The saptaka was completed with the addition of the the upper seventh krusta before prathama and the lower sixth atisvarya after mandra. The samans were sung in a descending order. Vedic chanting and the singing of the Saman were two separate musical styles.
The notes were associated with the Vedic metres: anustup, gayatr, trstup, brhati, pankti, usnik and jagati (SR 1.3.58-59).
The metres are central to the Vedic hymns. Although, the above sequence seems to be jumbled up in terms of the lengths of the metres, with its ratios of 8, 6, 11, 9, 10, 8, 12, I think that the ratios of the notes may have had something to do with the syllables in the metres. One sequence that is plausible is:
24, 27, 30, 32, 36, 40, 45, 48
corresponding to gayatri(24), usnik (28), atisakkari(30 for half), anustup (32), brhat (36),pankti (40), trstup (44), and jagati(48). A sequence of the metre names is given in NS 15.43-49.
The Paniniya Siksa (PS 12) maps the Vedic notes to the seven svaras:
uddate nisadagandharavanuddatte rsbhadhaivatau
svaritahprabhava hyete sadja madhyama pancamah
Of the seven musical notes nisada and gandhara can arise in the high pitch (udatta), rsabha and dhaivata in the low pitch (anudatta), whilesadja, madhyama, and pancama have their source in the medium pitch (svarita).
The same thing is said by the Naradiya Siksa (NarS 1..8.8) and the Yajnavalkya Siksa(YS8).
In NarS 1.5.1-2, Narada equates the tones of the venu ute to the seven notes of the sung saman:
yah samaganam prathamah sa venormadhyamah svarah
yo dvitiyah sa gandharastrtiyastvrsbhah smrtah
caturthah sadja ityahuh pancamo dhaivato bhavet
saste nisado vijneyah saptamah pancamah smrtah
In other words, the order is ma, ga, ri, sa, dha, ni, pa ,which isthe standard saptaka in descending order excepting for a transposition of dha and ni
The gramegeyagana and the aranyegeyagana of the Samaveda provide a musical notation for the melodies. The Brahmanaandthesutra literature also has references to singing and playing of musical instruments. Narada of the Naradiya Siksa associates musical notes with deities, social classes, animals, colours, and with fingers.
The notes with 4 srutis are called brahmana, with 3 srutis are termed ksatriya, with 2 srutis are termed vaisya, and the half-notes are called sudra (NarS 1.4.3-4). SR 1.3.53-55 says: “Sadja, madhyama, and pancama are brahmins, rsabha and dhaivata are ksatriya, nisada and gandhara are vaisya, while the notes antara-gandhara and kakali-nisada are sudra.
The classification of the notes as the sounds of the deities is as (NarS 1.4.13-14): sa is Agni’s, ri is Brahman’s, ga is Soma’s, ma is Visnu’s, pa is Narada’s, dha and ni are Tumburu’s notes.
Their respective colours are: red, pale yellow, golden yellow, sparkling white, black, plain yellow, and variegated (SR 1.3.54-55).
The Chandogya Upanisad (CU) has a considerable discussion of the structure of samans. While examining this material, it should be noted that the Vedic system of knowledge is recursive and what is described at a gross level is also applicable at a finer level.
CU 2.10 informs us that the seven-fold saman has 22 parts. The counting is done in terms of the syllables of the names of the seven parts of the saman which are hinkara, prastava, adi, udg tha, pratihara, upadrava, and nidhanaTheir individual syllable counts are 3, 3, 2, 3, 4, 4, 3, respectively.
Although this division of the saman is for the different parts of the song, the recursive system at the basis of Vedic narrative could suggest that it was also applied to notes. If that were the case, we find an exact match with the division of the srutis for the gandharagrama.
As to the special signi cance of the number 22, CU 2.10.5 says:
ekavimsatya”dityamapnotyekavimso va ito’ savadityo dvavimsena paramadityajjayati tannakam tadvisokam
With twenty-one intervals (syllables) a man reaches the sun, for the sun is the twenty- rst from here. With the twenty-second he conquers what is beyond the sun, that is glory, that is freedom from sorrow.
Other very early texts describing music include the Markandeya Purana (chapter 23), Dev mahatmya Purana (chapters 81-93), and the Vayu Purana (chapters 86-87).
The division of the saptaka
To return to the question of the division of the saptaka, consider the fixed ratio of 1.104 which takes us through the range in seven steps, as a straight- forward calculation will show. In a similar manner, one sruti in the series of 22 represents a ratio of 1 : 032. Table 3 presents a match between the two series:
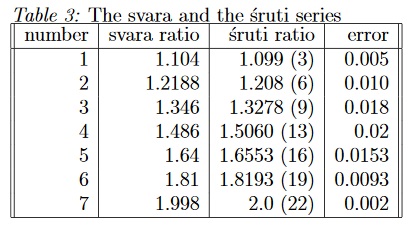The match is excellent. The error between the two series is extremely small. The mapping maps the srutis in groups of 3, 3, 3, 4, 3, 3, 3.
If one takens 21 srutis instead of 22, the match turns out to be even closer, as expected. For this the ratio for each sruti is 1.0336. This theoretical exercise shows that the saptaka couldn’t have been divided in this fixed manner. Neither could this reasoning have been at the basis of the choice of 22 srutis. The view that the srutis are non-uniformly distributed is supported by this calculation.
The number of ragas
A raga must have a combination of rising (aroha) and falling (avaroha) notes that are at least five in number. The combinations of pentatonic are called auduva, of hexatonic sadava, and of heptatonic sampurnaIn addition, there are the sadharanatanas (NS 28.32-36). Without going into further con-straints { and there are many of those {, the combinations of ragas that are obtained are as follows (Table 4):[8]
This number, as we mentioned before, equals 22 2
The sruti interval
Alain Danielou suggests[9] that the sruti interval is the comma diesis 81/80, defined as the difference between pa considered as the upper fourth from ri, and pa as the lower fourth from sa. Vidyasankar Sundaresan[10] argues that one sruti should rightly be the ratio 256/243. Danielou presents[11] a detailed reconstruction of the intervals of the 66 srutis.
Although we cannot be certain as to what precise ratios were used by Bharata, scholars have argued that 22 srutis provide a natural division of the saptaka.
Coda
From the evidence we have reviewed, it appears that the question of the origin of the 22 srutis cannot be answered unambiguously. The choice could have been based on the significance of the number 22 that goes back to Vedic ritual, as a number that transcends the earth or the sun. The number 22 may have even been arrived at from 3 7 + 1 where the basic number is the 7 of the number of notes and the tripling is from the “three worlds” and the 1 represents the usual transcendence. Or it may be related to the capacity to distinguish the srutis and a division that provides cycles of fourths and fifths.
If the choice of the 22 srutis was based on the mapping of Table 3, then the original distribution of the srutis for the various svaras must have been uniform with a single exception. From there the mapping of Bharata in his Natya Sastra represented further development. But the evidence indicates that the srutis were not uniformly distributed. This is also clear from the fact that the transition from a five-tone octave to a seven-tone octave is not uniform.
On the other hand, the ratios as reconstructed by Danielou or Sundaresan indicate a logical basis to the division. Bharata may have received this logic from his predecessors, given the fact that the number 22 appears earlier in the Upanisads. It is plausible that it was part of the musical tradition before Bharata’s time.
In the Visnudharmottara Purana, Markandeya tells King Vajra that in order to learn the art of icon-making one needs to learn the art of dance, and the art of music before learning dance. Indian arts are interrelated not only at the level of aesthetic experience but also at the level of technique[12]. It is not surprising then to see the number 22 (and the related numbers of 11 and 33) appear in so many different contexts.
Concluding Remark
It is a matter of great sorrow that the foundational books of Indian music such as the Natya Sastra, the Brhaddesi, the Sangita- Ratnakara are either out of print (the Manomohan Ghosh edition; the Satguru edition which is in print is deficient), never published in a critical edition (BrhadD), or published in an incomplete edition (SR).
Notes and References
[1] Manomohan Ghosh, The Natyasastra. Vol. 1, Manisha Granthalaya, Calcutta, 1967; vol. 2, Calcutta, 1961.
R.K. Shringy and Prem Lata Sharma, Sangita-Ratnakara of Sarngadeva, Vol.1 and 2 (Chapters 1 to 4 of the 7 chapters of the book). Vol. 1, Motilal Banarsidass, Delhi, 1978; Vol. 2, Munshiram Manoharlal, New Delhi 1989.
Emmie Te Nijenhuis, Indian Music: History and Structure. E.J. Brill, Leiden, 1974.
Alain Danielou, The Ragas of Northern Indian Music. Munshiram Manoharlal, New Delhi, 1980.
- Chaitanya Deva, The Music of India: A Scientific Study. Munshiram Manoharlal, New Delhi, 1981.
Ernest G. McClain, The Myth of Invariance. Shambhala, Boulder, 1978.
Vidyasankar Sundaresan, “The Theory of 22 Srutis.” http://www.cco.caltech.edu/vidya/music/srutis.html
[2] Manomohan Ghosh, The Natyasastra. Manisha Granthalaya, Calcutta, 1967, Vol. 1, pages lix-lxv. See also, Kapila Vatsyayan, Classical Indian Dance in Literature and the Arts. Sangeet Natak Akademi, New Delhi, 1968, pages 199-205.
[3] See Note 1.
[4] Brhaddesi ; see also Shringy and Sharma, vol 1, page 404.
[5] Shringy and Sharma, vol. 1, pages 141-2.
[6] SR 1.4.1-5. See also Shringy and Sharma, op cit, vol 1, page 164.
[7] Swam Prajnananda, Historical Development of Indian Music. Firma K.L. Mukhopadhyay, Calcutta, 1960.
[8] Shringy and Sharma, op cit
[9] Danielou, op cit, page 29.
[10] Sundaresan, op cit
[11] Danieou, op cit, pages 31-36.
[12] Vatsyayan, op cit, pages 380-396. 12
This article has been republished with permission from the author.
Featured Image: YouTube
Disclaimer: The opinions expressed within this article are the personal opinions of the author. IndiaFacts does not assume any responsibility or liability for the accuracy, completeness, suitability, or validity of any information in this article.
Subhash Kak is an Indian American computer scientist notable for his Indological publications on the history of science, the philosophy of science, ancient astronomy, and the history of mathematics.