Most Readers are aware that the Indian civilization is among the oldest in the world, if not actually THE oldest. They are also aware that Indian astronomy shares and reflects the age and maturity of its civilization.
And though Readers may suspect that Indian astronomy has its wonders and mysteries, not many will be privy to the details of why exactly something is a wonder, or what exactly is mysterious about such and such.
Indeed, Indian astronomy does abound in wonders and unsolved mysteries, and in this new series of articles, which will run in parallel with the ‘Hijacking’ series, we will explore some of those mysteries and wonders, and also touch upon a few misconceptions in Indian astronomy.
The Reader is cordially invited to a journey into the depths of Indian astronomy; to marvel at its wonders; to ponder over its unsolved mysteries; and to deliberate over its misconceptions.
Misconception # 1 – The Obliquity (tilt) of the Earth’s Axis
It was after tea on a summer evening, and the conversation, which roamed in a desultory, spasmodic fashion from golf clubs to the causes of the change in the obliquity of the ecliptic …
(Memoirs of Sherlock Holmes, The Greek Interpreter)
Let us begin then by considering in this first article what is probably the most widespread misconception of all in Indian Astronomy.
This misunderstanding is so pervasive that, let alone the general public, even the experts have been taken for a ride.
The misconception, which has to do with the tilt, or obliquity, of the earth’s axis, also ranks among the most clever and successful obfuscations in Indian astronomy carried out by the European scholars of yesteryear. They skillfully achieved the difficult task of hiding the treasure in plain sight, so to speak.
Most Readers will know that the axis of the earth is tilted. But, tilted with respect to what? The answer is – tilted with respect to the Ecliptic Plane.
The plane of the earth’s orbit around the sun is called the ‘ecliptic plane’, because eclipses occur when the Moon enters this plane while coming in line with the earth and the sun.
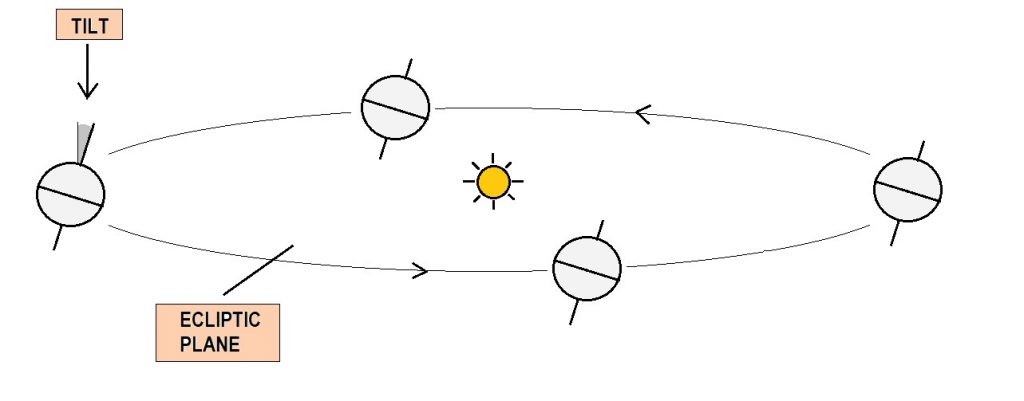
As seen in Fig. 1, the rotational axis of the earth makes an angle (tilt) of about 23.5 degrees to the axis of the ecliptic plane. The rotational momentum of the spinning earth keeps its axis pointing in the same direction in space, with the same tilt, as it travels around the sun.
Now, as you might expect, nothing in the universe is ever rock steady. Everything changes in time. Everything has periodic and non-periodic variations, including the tilt of the earth’s axis. Fig. 2 depicts the changing tilt of the earth’s axis in time.
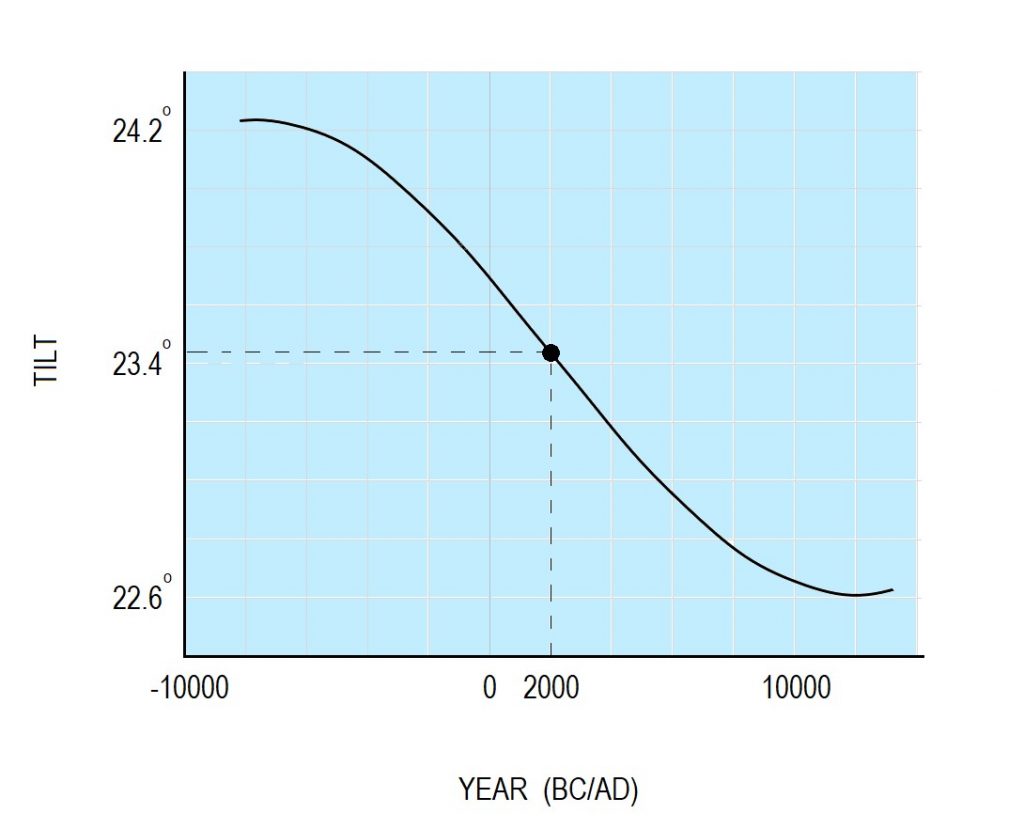
It is seen that the tilt varies between a low of 22.6° and a high of 24.2° in a slow cycle that lasts nearly 40,000 years. By a sheer coincidence we are currently (in 2000 AD) almost exactly in the middle of the cycle, with a tilt of 23.44 degrees (black dot).
As an aside, note that the earth’s tilt is of the greatest importance for the climate of our planet since the seasons are caused by this very tilt. Had there been no tilt, there would be no seasons, and every place on earth would have the same climate all year-round – a most undesirable thing! Also, more tilt implies a more extreme climate, and so we are not surprised when Geologists tell us that the last ice-age ended around 8000 BC, and the earth has been warming up steadily since.
Now, noting the steep variation of the earth’s tilt in time, we ask in curiosity – did the ancients measure and record the tilt of the earth’s axis? If they did, and if their measurement was accurate, that data would be invaluable for fixing that date in history.
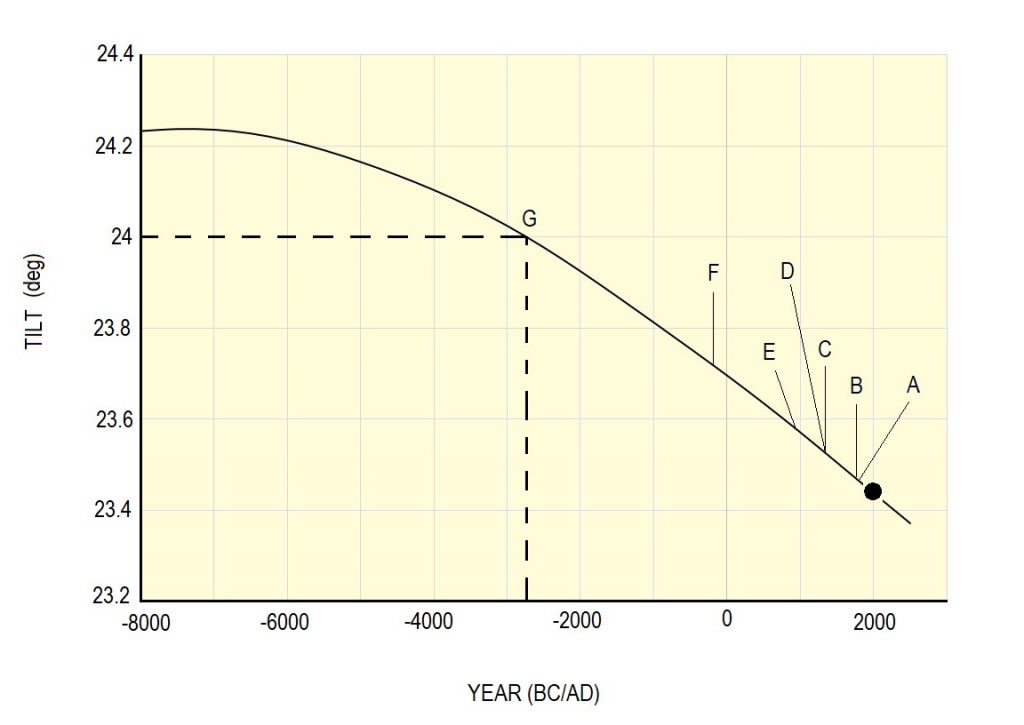
Let us look at a few samples of ancient recorded data, and where they fit on the tilt curve (Fig. 3).
| Reference | Date | By Whom | Tilt |
| • | 2000 AD | At present | 23.44° |
| A | 1814 AD | Gauss (European) | 23.46° |
| B | 1738 AD | Cassini (European) | 23.47° |
| C | 1587 AD | Tycho Brahe (European) | 23.525° |
| D | 1424 AD | Samarkand (Islamic) | 23.52° |
| E | 830 AD | Baghdad (Islamic) | 23.56° |
| F | 230 BC | Greek | 23.855° |
| G | 3000 BC | Surya-Siddhanta (Indian) | 24° |
Note that the Greek value was recorded around 230 BC, but they measured it erroneously as 23.855°, whereas the actual tilt at the time was much lesser.
As regards the Indian value, it can be seen that the tilt given in the Surya-Siddhanta (SS) stands out noticeably among the other values – for two reasons.
Firstly, the SS tilt data is obviously extremely ancient – nearly 50 centuries old (3000 BC). Secondly, compared to the other values, it appears very imprecise. While the others have two or three decimal places, the Indian value is a whole integer. I mean, what are the chances that the tilt was exactly 24.00° when the ancient Indian astronomer measured it? Very, very unlikely.
And so it happened that the European scholars dismissed this Indian value of the obliquity as a sloppy effort of measurement.
Their two conclusions are as follows: 1) The ancient Indian astronomer was obviously a poor observer. His data is not to be trusted within 1 degree. Perhaps he had poor instruments, or perhaps he was not technically competent, or both. 2) The Surya-Siddhanta actually dates from 400 AD. The tilt at that date was 23.7°. The best the Indian could do, with his poor instruments and inadequate technical ability, was to record the tilt as approximately 24°.
And there, dear Reader, the matter rests, as of today.
Now, if you were to peruse the Surya-Siddhanta, you would be struck by a few things: 1) Very elaborate and elegant planetary models; 2) Very concise instructions; 3) Extremely precise data.
And you will be left a little bewildered.
For example, the value of the sidereal year is given as 365.2587565 days; the Moon’s apsidal period is 8.848778 years; its Nodal period is 18.6016 years, etc.
How in the world (you say to yourself) can the Surya-Siddhanta contain an imprecise value like 24° for the tilt, when all the rest of the data is super-precise?
Hmm … this warrants a deeper look. And you search out the verse in question (given below).
(Surya-Siddhanta: Chap II, Verse 28): “The sine of greatest declination is 1397 …”
The ‘greatest declination’ is another way of stating the obliquity of the earth’s axis. The value given (i.e. 1397) is what is known as an R-Sine (explained later). To get the obliquity in degrees, we have to take the inverse Sine of the ratio (1397/3438).
And so, we obtain the Indian obliquity value as, Sin-1(1397/3438) = 23.975182°.
Hey, now wait a minute (you say), that is not 24.00°. Who in the world declared that the Surya-Siddhanta gives a whole (and unprecise) 24° for the obliquity?!
At this point a European historian, like David Pingree for instance, will step in and instruct you, with a condescending look, that 23.975 or 24, its all the same. The inept Indian astronomer of old meant to say 24°, but gave the closest value he could think of.
While you’re scratching your head and thinking up a reply, let us take a detour, and examine the Indian Sine Table.
The Indian Sine Table
The Indian Sine Table qualifies as a wonder in its own right. We will examine it in detail in another article. For now, let’s focus on the issue being discussed.
The table contains 24 rows, as shown below, with the angle in each row incrementing by 3.75°, till it reaches 90°. The sine of each angle is expressed as an R-Sine (Radius-times-the-sine), which is nothing but the modern sine of the angle multiplied by 3438 (the standard Indian Radius).
Focus on the last two columns. The second-last column is a modern calculation of the R-Sine of the angle, while the last column is the Indian R-Sine value.
| MODERN CALCULATION | INDIAN |
| No. | Angle (deg) | Sine | x 3438 = R-Sine | R-Sine |
| 1 | 3.75 | 0.065403129 | 224.855958 | 225 |
| 2 | 7.5 | 0.130526192 | 448.749049 | 449 |
| 3 | 11.25 | 0.195090322 | 670.720527 | 671 |
| 4 | 15 | 0.258819045 | 889.819877 | 890 |
| 5 | 18.75 | 0.321439465 | 1105.10888 | 1105 |
| 6 | 22.5 | 0.382683432 | 1315.66564 | 1315 |
| 7 | 26.25 | 0.44228869 | 1520.58852 | 1520 |
| 8 | 30 | 0.5 | 1719 | 1719 |
| 9 | 33.75 | 0.555570233 | 1910.05046 | 1910 |
| 10 | 37.5 | 0.608761429 | 2092.92179 | 2093 |
| 11 | 41.25 | 0.659345815 | 2266.83091 | 2267 |
| 12 | 45 | 0.707106781 | 2431.03311 | 2431 |
| 13 | 48.75 | 0.751839807 | 2584.82526 | 2585 |
| 14 | 52.5 | 0.79335334 | 2727.54878 | 2728 |
| 15 | 56.25 | 0.831469612 | 2858.59253 | 2859 |
| 16 | 60 | 0.866025404 | 2977.39534 | 2978 |
| 17 | 63.75 | 0.896872742 | 3083.44849 | 3084 |
| 18 | 67.5 | 0.923879533 | 3176.29783 | 3177 |
| 19 | 71.25 | 0.946930129 | 3255.54579 | 3256 |
| 20 | 75 | 0.965925826 | 3320.85299 | 3321 |
| 21 | 78.75 | 0.98078528 | 3371.93979 | 3372 |
| 22 | 82.5 | 0.991444861 | 3408.58743 | 3409 |
| 23 | 86.25 | 0.997858923 | 3430.63898 | 3431 |
| 24 | 90 | 1 | 3438 | 3438 |
On comparing the two columns, the Reader will no doubt be suitably impressed by the accuracy of the Indian Sine Table. For our current purpose though, the more significant observation is that the Indian R-Sines have been rounded-up, or rounded-down, to the nearest 1/3438 value.
This is an important observation which bears repeating: The precision of the Indian R-Sine is 1/3438.
That said, let us calculate the R-Sine of 24 degrees. We obtain, sin (24) x 3438 = 1398.36.
Well, well, what do you know! The modern R-Sine of 24 degrees is 1398.36.
And knowing that Indian R-Sines are rounded-up or rounded-down to the nearest 1/3438, the Surya-Siddhanta would have stated 24° as either 1399 (rounded up), or 1398 (rounded down), but never 1397!
That is, 24 degrees can never be represented as 1397 in the Indian system.
Colonial Deception
Back in 1813 AD, giving in to the demands of the clergy, the East India Company had lifted restraints on religious activity in India, thus setting into motion an aggressive campaign of Christian missionary work in the vast new colony.
One of the tentacles of this many-fronted activity consisted of the systematic deprecation of Indian mathematics and science, in particular, the deprecation of Indian astronomy, which was seen as the right-arm of the Hindu religion.
Starting in the early 1800’s, western scholars cast their attention on several problematic areas in Indian astronomy that stood in the way of a ‘final solution’, to permanently put the Indian science in its place. The 24-degree tilt was identified early on as a high priority, as it directly indicated a period around 3000 BC, which, apart from causing conflicts with Christian theology, also gave Indian astronomy and Indian civilization the unwelcome halo of a very ancient culture.
Some of these scholars suggested that the Indians were actually poor observers, and thus they recorded 24-degrees where the actual tilt was much lesser. But that suggestion would not quite jell, because a lot of Indian data, like the mean motions of the planets and the Moon for example, was highly accurate.
Others suggested (like the example below1), that the Indians had a ‘habit’ of rounding numbers!
According to Mr. Bentley, the Hindu astronomers (unless in cases where extraordinary accuracy is required) make it a rule, in observing, to take the nearest round numbers, rejecting fractional quantities: so that we have only to suppose that the observer who fixed the obliquity of the ecliptic at 24 degrees, actually found it to be 23 and 1/2.
In 1858, the 24-degree deception was finally set in stone by Prof. Dwight William Whitney and his Committee, which brought out the first English translation of the Surya-Siddhanta. They translated the above verse as follows:
The greatest declination, that is to say, the inclination of the plane of the ecliptic, is here stated to be 24°, since 1397 is the sine of that angle.
Since then, Whitney’s translation has been the benchmark among historians, both Western and Eastern, who have blindly accepted his statement.
And in this casual manner, the colonial scholars managed to trivialize and hide in plain sight the most direct proof of the great antiquity of Indian astronomy. Their success can be gauged from the fact that no one bothered to verify this for the past 150 years!
Misconception Summary
The obliquity, or tilt, of the earth’s axis is given as 23.975 degrees in the Surya Siddhanta, which was ‘nudged’ to 24 degrees whole by the colonials, thereby trivializing and obfuscating one of the fundamental markers of the antiquity of Indian astronomy.
From the obliquity curve, a tilt of 23.975° indicates a period around 3000 BC, which is very close to the accepted date of the Kali-Epoch, namely 3102 BC.
Action Needed
The 24-degree misconception regarding the Indian obliquity exists today in a wide spectrum of media like books, journals, articles, conference papers and videos. The Indian public and intelligentsia must challenge this, and counter any attempts by western historians to keep trivialized the ancient Indian obliquity data as an imprecise 24 degrees. Further, it must be universally acknowledged that this obliquity value dates from 3000 BC.
Postscript
Having seen that the obliquity data in the Surya-Siddhanta dates from 3000 BC, we are naturally curious to know if any other data in Indian astronomy points to the same period.
We currently know of at least 3 other items in Indian astronomy that point to 3000 BC, or thereabouts.
1) The value of the Sun’s equation-of-center given in the SS indicates a time range of 3000 BC or older;
2) The ubiquitously mentioned pole-star in Indian astronomy and literature, namely Dhruva (modern name Thuban), indicates a period about 3000 BC;
3) It is mentioned in the Satapatha Brahmana text that the Krittika Nakshatra rises exactly in the East, which occurred only in ancient times, around 3000 BC. Nowadays Krittika rises between East and North-East.
We will discuss these in other articles.
References
- The History of British India, Vol. 1, James Mill, 1817, page 418.
Featured Image: Research Matters
Disclaimer: The opinions expressed within this article are the personal opinions of the author. IndiaFacts does not assume any responsibility or liability for the accuracy, completeness, suitability, or validity of any information in this article.
Anil Narayanan is former scientist at ISRO, now working as a consultant in Washington DC. His hobby is ancient astronomy to which he devotes most of his spare time. He is the author of the book ‘History of Indian Astronomy: The Siamese Manuscript’.

